linear palette extraction
category: code [glöplog]
does anyone here know a formula/technique to generate a linear color palette from random r, g, b colors? i just briefly looked at the subject and thinking. my concern is that its not possible to differentiate between the |r-g|, |r-b| and |b-g|, but if one separates these individually it might work? i have not written any code just yet.
use hsl and convert back to rgb?
http://www.fastcolabs.com/3002676/open-company/magical-tech-behind-paper-ipads-color-mixing-perfection
In this article, they mention a paper by a german scientist about a 6D space when colors blend well... "Ein Beitrag zur Optik der Farbanstriche"
Never found a pdf.
In this article, they mention a paper by a german scientist about a 6D space when colors blend well... "Ein Beitrag zur Optik der Farbanstriche"
Never found a pdf.
rudi: Maybe you could calculate for each color the average intensity, i.e. (r+g+b)/3, so you can order the colors by brightness. At least that would be a valid ordering.
(Of course you need not even make the division by 3, just sum up r+g+b.)
psenough: true true. one could compare the hue values. i didnt think of that.
how many colors? i just thought about a tetraeder representing a volumetric mixture of all shades and blends of 4 colors. i dunno howto pic the right voxel tho. :D
well. my current is red, magenta, gray, blue, white and cyan (in different brighnesses and saturations). although i want a formula to separate all colors so that if all colors are used one gets a hue-gradient. the problem lies in separating the saturation and brightness versus the hue to a gradient. but maybe there is a optimal way to do this without using higher dimensions and advanced math. im not sure what you mean by blend?
ahh okay. so... by palette you mean something like 256 colors and lots of asort colors?
straight decimal value sort maybe? or start with buckets of red, green, blue weights and then bubble by component colorweights or average luminance.
straight decimal value sort maybe? or start with buckets of red, green, blue weights and then bubble by component colorweights or average luminance.
Do you want to create a 256 colors palette with a gradient from any of your fixed color ( red, magenta, gray, blue, white, cyan1, cyan2, ... ) to another ?
Do the brutal way: compute a 32 or 64 shades gradient for each combination ( e.g. from red to magenta, then red to gray, .... until cyan2, to whatever ) and extract the 256 most unique colors, keep the mapping from the original gradient color to the final palette.
Super oldschool style :p
Do the brutal way: compute a 32 or 64 shades gradient for each combination ( e.g. from red to magenta, then red to gray, .... until cyan2, to whatever ) and extract the 256 most unique colors, keep the mapping from the original gradient color to the final palette.
Super oldschool style :p
going to HSL space sounds great. then sort colors into various hue buckets, then sort on brightness, done.
If you don't need to display the palette in a nice way, just handle it as a 3D palette (which is what RGB, HSL etc. are).
If you do, do what Oswald said (but sort on saturation inside the hue buckets which is missing).
If you do, do what Oswald said (but sort on saturation inside the hue buckets which is missing).
another one: make a 3d Hilbert curve going through the rgb cube, and use it to index your colors.
mmh. i have painted a result. nice 256x256 palette. a simple 5x3 box scaled up to 256x256. but i can't figure howto do this coded wise. it's a basic half hue cycle red magenta blue and cyan. but the grey shades are definetely the special case not making it work cause it's no real color in the cycle and you have to add it manually. :/
iq: what is a 3d hilbert curve? or how can it be used.
not to confuse those who didnt know what i really was out after.
here is an example taken from this site: http://lodev.org/cgtutor/plasma.html
say one has any image of different colors, in this case a plasma:
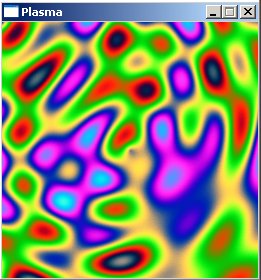
and one would like to extract the palette in the following way:

now the code is on that page to generate a palette lookup, but if one didnt have one.
so yes. its for a 256 color palette, but it doesnt matter what sizes it is, since the algorithm should take any amounts of colors.
not to confuse those who didnt know what i really was out after.
here is an example taken from this site: http://lodev.org/cgtutor/plasma.html
say one has any image of different colors, in this case a plasma:

and one would like to extract the palette in the following way:

now the code is on that page to generate a palette lookup, but if one didnt have one.
so yes. its for a 256 color palette, but it doesnt matter what sizes it is, since the algorithm should take any amounts of colors.
This doesn't really look like a "linear" palette but more like "palette that preserves the distances between pixels of each color in the image".
You could somehow calculate the minimum (or average?) distance between two distinct colors and use that as a weighting and try to find neighboring colors that way. Two probably very stupid idead that cross my mind:
1. Treat all colors as particles in 1D with spring physics. Add springs between particles which have a rest length of the pixel distance between the two colors... and then let the system try to relax (eg. with the good old Verlet integrators). If it seems relaxed enough, just order the colors by their 1D particle positions.
2. Or you can always use the distance between colors as dataset that you then try to solve with the Travelling Salesman. Of course it's prohibitively slow for 256 nodes but there's heuristics that make things easier, eg. Simulated Annealing.
You could somehow calculate the minimum (or average?) distance between two distinct colors and use that as a weighting and try to find neighboring colors that way. Two probably very stupid idead that cross my mind:
1. Treat all colors as particles in 1D with spring physics. Add springs between particles which have a rest length of the pixel distance between the two colors... and then let the system try to relax (eg. with the good old Verlet integrators). If it seems relaxed enough, just order the colors by their 1D particle positions.
2. Or you can always use the distance between colors as dataset that you then try to solve with the Travelling Salesman. Of course it's prohibitively slow for 256 nodes but there's heuristics that make things easier, eg. Simulated Annealing.
rudi: what you're showing there isn't so much a palette as a colour gradient. One that's designed by hand. You won't reconstruct that by hue ordering I suspect - you might get some nice alternatives, but I doubt you'll match the original order.
If you want to reconstruct a palette like that I guess you have to look for colours that occupy adjacent pixels - that implies they are close together in the gradient.
It's probably quicker/easier to do this by hand (or just make a similar gradient in photoshop or whatever) unless you want to do it for lots of images.
If you want to reconstruct a palette like that I guess you have to look for colours that occupy adjacent pixels - that implies they are close together in the gradient.
It's probably quicker/easier to do this by hand (or just make a similar gradient in photoshop or whatever) unless you want to do it for lots of images.
kb_: yes, sorry if i was a bit loose by the term linear. i really like your ideas especially number one. i was heading for that direction. for some simpler solution rather than complicated math that i dont know anything about.
1. Find all distinct colours.
2. For each pair of colours calculate a distance metric from the picture. (e.g. averate distance for the closest pixel
in the one set for each pixel in the another)
3. Find the shortest path that connects all the colors using the said metric.
2. For each pair of colours calculate a distance metric from the picture. (e.g. averate distance for the closest pixel
in the one set for each pixel in the another)
3. Find the shortest path that connects all the colors using the said metric.
s/for/to/
kb_: Was Statix this ... raw ? I thought he used the classic approach of having a 256x64 or 256x256 LUT mapping each color at different brightness. Or maybe he used the Quake 1 approach.
rudi: Nice that you clarified what you're looking for because it wasn't clear at all from your previous post :p
rudi: Nice that you clarified what you're looking for because it wasn't clear at all from your previous post :p
The Neuquant algorithm does more or less what kb described, but instead of a spring network it uses a neuronal network chain that 'learns' to cover the color-space of your input image.
The output of the palette will be a gradiant with some noise on top of it. You can remove the noise if you want a more 'how graphican would design the palette' output.
The algorithm: http://members.ozemail.com.au/~dekker/NEUQUANT.HTML
The output of the palette will be a gradiant with some noise on top of it. You can remove the noise if you want a more 'how graphican would design the palette' output.
The algorithm: http://members.ozemail.com.au/~dekker/NEUQUANT.HTML
Hilbert curve fills the plane/space, it's one space filling curve amongts other, and can be used to convert from 2d/3d/Nd to 1d (compression, error diffusion...):


As for your problem, don't know if the following is correct, but anyway:
Pick the "highest" (definition?) pixel.
Set it as "seen", as well as all pixels of this color. Put this color as first in a color table
Track all the "unseen" pixels on the edges of the "seen" pixels, get the one which has greatest occurence as next in your color table. Set all the pixels with this color as "seen", etc...
Problem is that you must start with an extremity of your color table ("highest") (which may well have no extremities!). Otherwise you will have to define interior/exterior which might be tricky with unconvex shapes. And it might not work... :p Advantage is that it sounds simple.
Pick the "highest" (definition?) pixel.
Set it as "seen", as well as all pixels of this color. Put this color as first in a color table
Track all the "unseen" pixels on the edges of the "seen" pixels, get the one which has greatest occurence as next in your color table. Set all the pixels with this color as "seen", etc...
Problem is that you must start with an extremity of your color table ("highest") (which may well have no extremities!). Otherwise you will have to define interior/exterior which might be tricky with unconvex shapes. And it might not work... :p Advantage is that it sounds simple.
